US Physics: Pulsed-Wave Doppler Simulation

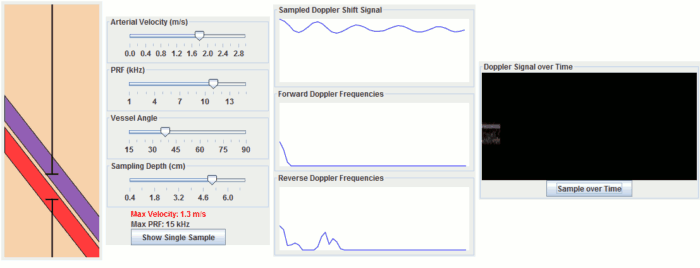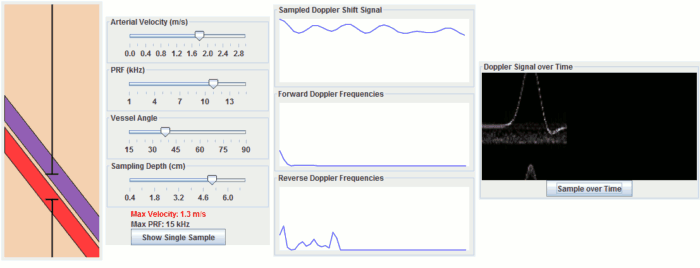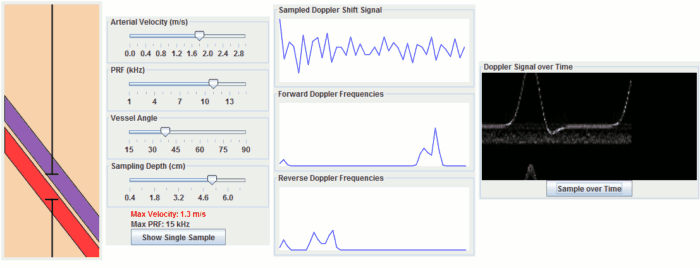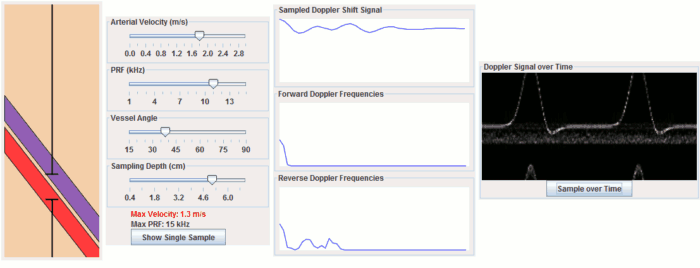
This Doppler simulation illustrates how pulsed doppler ultrasound works. It contains a simulated artery and vein and allows you to move the sample volume and adjust parameters such as PRF, flow angle, and arterial velocity. Click "Show Single Sample" to simulate sampling a single timepoint to find the instantaneous velocity. Click "Sample over Time" to simulate sampling multiple timepoints with blood flowing. If your browser does not have Java (e.g. iPad), you can click on some of the sliders and the two buttons to see examples.

Explanation

Ultrasound relies on reflected pulses of sound waves to identify the location of objects in the body. It turns out that moving objects change the characteristics of these sound waves as well. This is termed the Doppler effect (some sources argue about whether what is measured actually represents the classical Doppler effect, but the equation is the same). Typically we talk about the Doppler effect causing a change in frequency of an incident sound (or light) wave related to the difference in velocity between the sender and receiver:

Δf = v/c * f₀

where v is the velocity difference, c is the speed of sound, f₀ is the transmitted frequency, and Δf is the change in frequency.

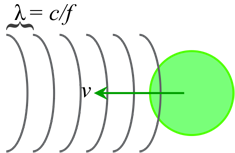
Note that in Doppler ultrasound, since we are transmitting and then receiving a reflection, the actual shift is twice the shift written above. Now, it would be very convenient if we could just send a signal and measure the frequency of the Doppler shifted signal that we get back. Unfortunately, lots of other signals could be in the way, like an overlying vein or an artery just behind where we want to measure. Since we would be beaming in sound, we'd get the Doppler shifts from all of these signals. How do we overcome this? Pulsed-wave Doppler.

Pulsed-wave Doppler sends short sound pulses and waits for them to come back. Just like with regular grayscale ultrasound, we can determine the depth by how long it takes to come back. The 'sample gate' that we can move on our ultrasound machine sets which depth we are listening for. Because these pulses are very short, we cannot measure their frequency shift. Instead, we measure what's termed a phase shift - this represents a shift in the time of a sinusoid. It turns out that for the exact same reasons that moving signals cause frequency shift, if you measure their returned signals at a single instant in time, you measure an instantaneous phase shift. By measuring these phase shifts over time (with multiple pulses very close together), you then get the Doppler frequency shift.

Importantly, the rate at which we measure, or sample, the Doppler shift determines how well we can measure it; this number is known as the pulse repetition frequency or PRF. We have to sample the Doppler shift at least twice as frequently as the highest frequency shift that we want to measure - this is called the Nyquist rate. If we sample it too infrequently, we get a phenomenon known as aliasing, where we measure the wrong frequency (in fact, often the reverse frequency shift). This is the exact same phenomenon responsible for aliasing in MRI, where if we set our FOV too small, we get wrap from the edges; it is also important in Phase-Contrast MRA. You can calculate the maximum measurable frequency and therefore velocity easily:

2 * Δf_max = PRF and Δf = 2 * v/c * f₀

so that v_max = PRF / (4 * c * f₀)

So why can't we just crank up the PRF? Well, remember - in ultrasound we have to send in pulses and wait for them to come back. If we sent in two pulses before waiting for the first one to come back, we wouldn't know which echo came from which pulse - and so we couldn't figure out the right depth. So the PRF has to be set long enough to wait for a pulse to get to the depth we want and come back:

c = depth / t so t_PRF = 1/PRF = 2 * depth / c

or PRF_max = c / (2 * depth)

remembering that PRF is a frequency so that 1/PRF is a time.

Wall filter. As you may notice from the simulation, a doppler signal is still generated from non-moving tissue. This is partly because of noise but also because of motion of other objects, such as nearby objects (e.g. liver near the heart) or your hand holding the transducer. We need to remove this extraneous signal by filtering it out. This filter is called the wall filter and it removes low-frequency (thus, low velocity) signals. You can change the parameters of the wall filter on the ultrasound machine to set its threshold.

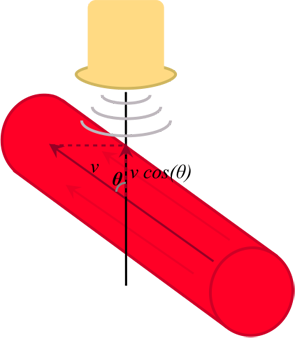
Angle effects. So far we have been assuming that the blood is flowing directly towards the ultrasound transducer. In practice, this is almost never the case, so we have to correct for the direction of blood flow. This is done with simple trigonometry; if θ is the angle between the ultrasound beam and the blood flow, then the component of velocity towards the beam is

v_towards = v * cos(θ)

Things to remember:

• The Doppler shift is a change in frequency (and phase) of the reflected signal by a moving object.
• The Doppler equation usually written in ultrasound textbooks is: Δf = 2 * v * cos(θ) * f₀ / c
• The pulse repetition frequency (PRF) must be twice as high as the expected maximum Doppler shift. If sampling is too slow, then velocities will alias to negative.
• The maximum highest PRF is determined by the depth (how long it takes a signal to go and return).

References

• Jensen JA. "An analysis of pulsed wave ultrasound systems for blood velocity estimation." Acoustical Imaging 22, pp. 377-384, 1995. link
• Bushberg, JT, et al. The Essential Physics of Medical Imaging. 3rd ed. Wolters Kluwer.

DopplerSim Applet copyright 2014 Mark Hammer. All rights reserved.