X-Ray Physics: X-Ray Interaction with Matter and Attenuation

This simulator illustrates the effects of changing tube voltage in fluoroscopy or radiography on patient dose and image contrast. You can also alter the body part thickness. Air kerma (K_ar) reflects the change in photon flux necessary to obtain the same exposure (image noise). Dose is the dose to the patient for the same image noise; note that this dose is a first-order approximation and does not take into account secondary scatter events. The x-ray tube is a (very) gross approximation of a tungsten anode with 2.5 mm Al filtration.

Tube Voltage 50 60 70 80 90 100 110 120 130 140 150 kV Patient Thickness cm    Soft tissue Transmission % (Attenuation %) Compared to 100 kV and 20 cm patient: Kar :1    Dose :1 to obtain the same image quality Iodine/Soft tissue Contrast :1   Muscle/Fat Contrast :1
X-Ray Spectra Your browser does not support the HTML Canvas.	Transmitted X-Ray Intensity Your browser does not support the HTML Canvas.	Simulated Image Contrast Your browser does not support the HTML Canvas.

Left: X-ray spectra; Blue, Tube beam spectrum. Orange, transmitted beam spectrum (scaled to have the same intensity). Middle: X-ray intensity passing through the patient (white = strongest radiation, black = weakest). Right: Simulated image contrast with fat, muscle, and iodinated contrast in a vessel. This contrast does not take into account the effects of scatter.

X-Ray Interaction with Matter

In order to understand the means by which we see contrast in an x-ray image - i.e. the difference between fat, muscle, bone, and iodinated contrast - we need to understand how x-rays interact with matter. X-rays are simply high-energy photons (produced by bombarding an metallic anode with electrons).

X-Ray Tube. There are two primary means by which we can change the x-ray beam produced by the tube: altering the current (mA) and altering the volage (kV). The current (measured in and often referred to as mA, or milliamperes) across the tube determines how many electrons are released to strike the anode. Increasing the mA will increase the number of electrons that strike the anode, with a consequent linear increase in the number of photons produced by the tube. The voltage across the x-ray tube (measured in and often referred to as kV, or kilovolts) affects the velocity of the electrons as they strike the anode; this affects the energy of the photons that can be produced by the tube. Additionally, higher velocity electrons will produce more photons, something on the order of (kV)³.

While I will not go into detail here, know that there are two contributions to the x-ray spectrum produced by the tube: Bremsstrahlung radiation and characteristic x-rays. Bremsstrahlung radiation is a continuum with maximal energy at a keV = tube kV. The most photons produced occurs at ~0 keV and almost no photons are produced at keV = kV. Characteristic x-rays are due to electron ejection events; the hole is filled by another electron, which emits an x-ray at a specific frequency. Each element will have one or a couple relevant characteristic x-rays, which are produced at a higher rate compared to the Bremsstrahlung at any frequency (but with a very narrow peak). Because of tube filtration, the very low energy photons are removed and do not reach the patient. Note that the average energy of the beam is much less than the peak energy; a rule of thumb is that it would be 1/3 of the maximum energy.

X-ray interaction with matter. Again, without going into the gory detail here, we need to know that there are two major ways in which diagnostic x-rays interact with tissue. The first is the photoelectric effect, where a photon uses up all of its energy to eject an electron from an atom; while the electron will move around and ionize neighboring atoms, there are no scatter photons. The second major effect is Compton (incoherent) scatter, where a photon hits an atom and ionizes an electron but does not use up all of its energy. The photon then scatters in a different direction with a bit less energy, and the free electron goes about doing damage. Scattered photons can travel back towards the tube, pass through the patient and hit the detector from any odd angle, or scatter again within the patient.

Each time a photon ejects an electron - ionizes an atom - this creates free radicals that can damage DNA and wreak havoc. The energy that a tissue absorbs from photon interactions is referred to as dose. For a discussion of different measures of dose, see the CT Dose section or the briefer discussion in the Radiography section. For this discussion, just remember that dose is energy per kilogram of tissue - and that more of it is bad. Also, know that another word for dose is kerma (kinetic energy released in matter).

X-ray beam attenuation. As the x-ray beam passes through tissue, photons get absorbed so there is less energy; this is known as attenuation. It turns out that higher energy photons travel through tissue more easily than low-energy photons (i.e. the higher energy photons are less likely to interact with matter). Much of this effect is related to the photoelectric effect; the probability of photoelectric absorption is approximately proportional to (Z/E)³, where Z is the atomic number of the tissue atom and E is the photon energy. As E gets larger, the likelihood of interaction drops rapidly. Compton scattering is about constant for different energies although it slowly decreases at higher energies. We'll discuss the means by which these effects generate tissue contrast later, but just realize here that they are responsible for the different absorption of photons at different energies.

Beam hardening. As I mentioned, the low energy x-rays are stopped much more quickly than the high-energy photons. Thus, what comes out of the tissue is mostly the high energy photons (see the simulation, left panel). This is referred to as beam hardening (a soft beam has mostly low energies). The amount of radiation that passes through tissue is given by the Beer-Lambert law, which says that

Intensity(out) = Intensity(in) * e ^{-(μ * d)}

where μ is the linear attenuation coefficient and d is the distance the photon has to travel through the tissue. The linear attenuation coefficient μ varies by photon energy (decreasing) and by the material (see below).

Energy deposition. As the beam is attenuated - and thus deposits energy (dose) in the patient - the amount of energy left is less, and the average energy is higher so fewer interactions occur. Both of these effects result in decreasing energy deposition from the skin to the back of the patient. In other words, much of the dose is deposited near the skin. This is why the deterministic effects we are worried about relate to skin injuries (the other reason being that the skin is a particularly sensitive organ). Larger patients, who require higher doses to penetrate through the larger body parts, are at higher risk of skin injuries.

Attenuation and Dose

As you can see from the Beer-Lambert equation, the amount of photons passing through an object drops off rapidly (exponentially). This is illustrated in the middle panel of the simulation. The thicker the patient or body part, the fewer photons escape to the other side. We need a certain number of photons to produce an image. Back in the days of film, you needed a certain exposure to develop a particular type of film (this was referred to as the film's ISO). While digital detectors have a much higher dynamic range (just like your digital camera, they can operate at basically any ISO), there is still a minimum number of photons necessary to create a useful image.

Noise. Why do we need a certain number of photons to make an image? Realize that each photon being produced is a random event (we're not tracking one photon that goes into the patient to see if it comes out the other side - we just see how many photons come out). The possibility of a photon interacting with the tissue and scattering is random as well. Thus, our image is actually made up of millions of random events. In any random process, there are fluctuations (that's why it's random!). We need a large enough number of photons to be sure of what our picture looks like - in other words, we need enough photons so that our image is brighter than the noise of fluctuations. It turns out that in x-rays,

SNR ∝ √N

where SNR is the signal-to-noise ratio and N is the number of photons. For a more detailed discussion, see the section on signal-to-noise in fluoroscopy.

kV and Dose. We have already discussed the fact that high-energy photons pass through tissue with less attenuation. While these photons create more damage when they do hit electrons in the tissue, it turns out that this is a relatively small effect. Thus, overall changing an x-ray beam to a higher energy will deposit less dose to the patient. In addition, because more photons are passing through, there are more photons to make our image - so it will be less noisy. Also, remember that when we crank up the kV, we get more photons from the tube itself (photons ∝ kV³). We can either keep those increases and enjoy our pretty picture, or, more commonly and charitably, we can actually drop the number of photons we send through the patient. Thus, when we increase the kV, we can decrease the mA or exposure time (mA * s product).

mA and Dose. Radiography and fluoroscopy systems have so-called phototimers that shut off the beam after they get enough photons for the desired noise settings. Thus, increasing mA means that the image will take less time (more photons per second -> fewer seconds). Note that x-ray tubes have a maximum mA because they can overheat. This is relevant in long angiography runs or in magnification mammography (where you have to use a small focal spot, which will overheat more quickly).

Patient Thickness and Dose. As we mentioned, far fewer photons will make it through a thicker patient - exponentially so. Therefore, we have to send more photons through in the first place (the phototimer will just wait). More photons means more likelihood to hit the tissue and thus more dose. Also, larger patients have more tissue for scattered photons to hit a second or third time, increasing dose. See how increasing the kV would really help in large patients - we have fewer tissue interaction events and better penetration, so we can use fewer photons and have less dose. As we will see below, though, it's not a free lunch - you have to trade-off between kV and image contrast. Play with the simulation to see how dose changes with kV and patient thickness.

Tissue Contrast

If all different types of tissue stopped x-rays in the same way, then we would have no picture - just a gray blob on our screen. The difference in x-ray penetration between different tissues represents the contrast in the image, i.e. how easily we can tell different objects apart. (I'm not going to get into a discussion of subject vs image contrast or contrast versus feature size; these can be found in other texts.) So why do different tissues stop x-rays differently?

Photoelectric absorption. We mentioned earlier that the probability of photoelectric absorption is proportional to (Z/E)³. What we did not discuss, however, is the concept of the k-edge. Albert Einstein won the Nobel prize for explaining how photoelectric events require a minimum amount of energy (enough to dislodge the electron); it turns out that this is also the most likely energy for those events to occur. Higher energy photons are much less likely to cause photoelectric events. The k-edge represents the energy needed to eject a K-shell electron (the innermost and most strongly bound electrons). Outer shell electrons have absorption edges but these are much too low energy to be relevant.

In soft tissues, the dominant elements (e.g. C, H, O, and N) have very low K-edges, in the range of a few keV. While these elements do contribute to the photoelectric effect and attenuate low energy x-rays, there is no relevant k-edge with its substantial change in attenuation. However, the elements iodine and barium have K-edges around 30-40 keV, right in the middle of the x-ray beam spectrum. Thus, soft tissues with even a small amount of iodine will have a much stronger x-ray stopping power than those without.

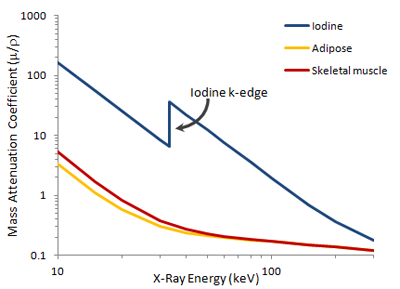
Mass attenuation coefficients for adipose tissue (orange), skeletal muscle (red), and iodine (blue) plotted on log-log axes. The k-edge of iodine occurs around 33 keV. Note that fat and skeletal muscle almost overlap except at very low x-ray energies.

Absorption due to Compton scattering is nearly independent of the X-ray energy. It does depend on the material (specifically, the electron density) but is still much less than the photoelectric absorption in diagnostic x-ray imaging. Compton scattering is responsible for the right-hand tail in the above graph. Note that it also creates scatter photons that may hit the image detector and contribute to background / noise (because they are scattered at different angles, we do not know where they initially came from).

Thus, the main contribution to differences in x-ray attenuation in diagnostic imaging is photoelectric absorption. You can see from this graph, though, that these differences are much more apparent at low energies. This is why lowering kV improves image contrast (with a trade-off of increased dose). The presence of materials with high k-edges such as iodine or barium improve the contrast at higher kV, but contrast is still better at lower kV. For example, a beam at 80 kV will have an average x-ray energy near 30 keV - exactly the k-edge of iodine.

Mammography

In mammography, we need to distinguish thin whisps of breast tissue or tiny calcifications from the surrounding fat. Soft tissue and fat attenuation curves are shown above; Calcium has a k-edge of 4 keV. In order to obtain image contrast with these materials, we need to utilize extremely low energy photons. (We also need very good spatial resolution, but that's another discussion.)

One way of obtaining a very low energy beam is to use a low kV. We also need to make sure that we have no filtration (which removes all of the low-energy photons we need). Many mammography units replace glass with beryllium as the window for the x-ray tube. Beryllium has a very low atomic number (Z=4) so its attenuation is less than glass; additionally, glass (mainly SiO₂) has a k-edge at 1.8 kV and higher atomic numbers (8 and 14), with increased photoelectric attenuation.

In addition to the low kV, we'd like a more efficient way of producing low-keV x-rays. Traditionally, this was done by using a molybdenum instead of tungsten anode. In order to understand why, let's go back to how x-rays are produced. One component is the Bremsstrahlung radiation, which depends simply on the tube voltage. The other component, which is more efficient, is the characteristic radiation. Characteristic x-rays represent those produced when an electron from the cathode knocks out an electron in an anode atom; another electron from a higher-energy orbital takes its place. This new electron releases an x-ray with the energy of the difference in binding energies of the two orbitals.

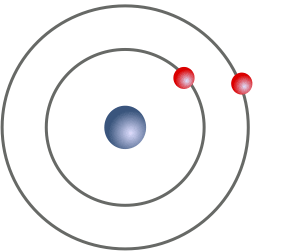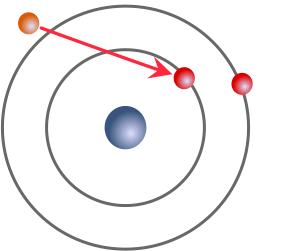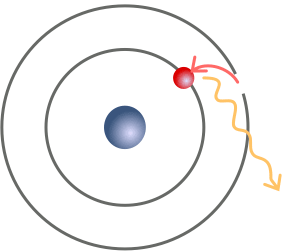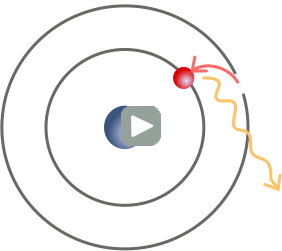
The characteristic x-ray production process. A high-energy electron (orange) strikes a k-shell electron (red) and knocks it out of the atom. An L-shell electron (also red) fills its place, releasing a photon (yellow) with energy equal to the difference in binding energies in the two orbitals.

Anode Material. For tungsten, the characteristic x-rays are around 60-70 keV, higher than what we want. For molybdenum, the characteristic x-rays are ~17.5 keV and 19.5 keV. These are in exactly the range we want to distinguish fat, soft tissue, and calcium. Now, we will still get the Bremsstrahlung radiation - but those high-energy x-rays will not contribute to contrast; we can get rid of them with a clever trick. We can use molybdenum as the filration material as well as the anode. The k-edge of an element will always be slightly greater than its characteristic x-rays (~ 20 keV).

Why is the k-edge slightly higher than the characteristic x-ray? The k-edge represents the energy needed to knock out a k-orbital electron (its binding energy). The characteristic x-ray represents the energy lost to dislodge a higher-orbital electron (typically L-shell) with much lower binding energy but also the energy gained by filling the k-shell (k-shell binding energy). Thus, the characteristic x-ray energy is the k-shell binding energy (same as k-edge) minus the L-shell binding energy (a small amount).

An alternative to molybdenum is rhodium, with characteristic x-rays at 20.2 and 22.7 keV and k-edge of 23.3 keV. This is often used for denser breasts, which require more penetration (in order to minimize the dose). Obviously, contrast is slightly worse. Now, more recently the manufacturer Hologic has introduced breast tomosynthesis which requires longer imaging times and more images. The longer times may overheat the molybdenum, and more images means more dose to the patient. In order to solve those challenges, that machine uses a tungsten anode with various filtration options including rhodium and aluminum; these combinations provide worse contrast but less dose. Advances in the imaging technology itself make up for the disadvantages, but it is a good lesson in the trade-offs necessary in x-ray imaging.

Things to Remember

• X-ray tubes produce photons by electron bombardment of a metallic anode. The resulting photon spectrum is a continuum and is determined by (a) characteristic x-rays (related to the anode material) and (b) Bremssrahlung radiation (related to the tube voltage, kV).
• The number of photons sent through a patient is determined by the current across the tube (mA) and the imaging time (s), which are sometimes multiplied together as mA*s = mAs. Changing kV changes the number of photons in a non-linear fashion ~ (kV)³.
• X-rays interact with tissue in 2 main ways: photoelectric effect and Compton scatter. To a first approximation, the photoelectric effect contributes to contrast while the Compton effect contributes to noise. Both contribute to dose.
• The photoelectric effect is highly accentuated at the k-edge of a material; materials with k-edges in the relevant range include iodine and barium. The k-edges are typically low energies, and the closer your x-ray energy is to the k-edge (as long as it is above it), the more likely a photoelectric event is to occur.
• Thus, to improve contrast, decrease your x-ray energy (kV). However, this increases dose because more x-rays are absorbed by the patient so you need to send more x-rays through from the tube. This represents the central trade-off in x-ray imaging.
• X-ray penetration is an exponentially decreasing function of patient thickness. Large patients get much larger doses; you can improve this by increasing the x-ray energy but at the cost of contrast.
• Lower energy x-rays are more attenuated for any given distance than high-energy x-rays. Thus, as the beam passes through material (either the filtration or the patient), it becomes harder, i.e. increases in average x-ray energy (while fewer x-rays come out at the end).

References

• Bushberg JT, et al. The Essential Physics of Medical Imaging. 3rd Ed. Section 3.3.
• Duncan JR and Panahipour S. "Tissue Attenuation of X-Rays." ImageWisely.org
• Mass absorption spectra obtained from NIST here.

---

Content and images copyright 2014 Mark Hammer. All rights reserved.